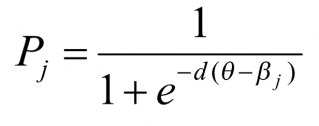Анализ результатов тестирования в процессе Rasch Measurement
Владимир Ким
Уссурийский государственный педагогический институт
Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Опубликовано в ж. «Педагогические Измерения», № 1, 2008. С.49-58.
Аннотация
В статье рассмотрены общие вопросы анализа результатов тестирования на основе одномерной модели Раша. Приведены эмпирические данные по тесту «Механика» для средних общеобразовательных учреждений. Показано, что экспериментальные данные удовлетворительно согласуются с моделью Item Response Theory (IRT).
Ключевые слова: тест, теория Rasch Measurement, педагогические измерения.
Педагогический тест как средство измерения учебных достижений может дать достоверный результат только в случае его корректного применения. Корректность применения теста – это многоаспектное понятие, включающее в себя вопросы конструирования и дизайна теста, вопросы разработки и применения тестов и, разумеется, интерпретации результатов тестирования. В данной работе основное внимание уделено вопросам корректности интерпретации результатов педагогического тестирования, проводимого на основе модели Г. Раша. Анализ результатов обычно проводится на основе классической теории тестов или на основе Item Response Theory.
После выполнения работ по созданию теста и сбора данных на репрезентативной выборке испытуемых, производится интерпретация результатов. Этот этап принципиально отличается от технологии, принятой, скажем в экспериментальной физике. Там экспериментальные данные пытаются описывать с помощью той или иной теории. Если теоретическая зависимость между исследуемыми величинами не соответствует наблюдаемой в эксперименте, то делается вывод, что теория недостаточно развита и требует дальнейшей разработки. В теории педагогических измерений может применяться иной подход. Если в физике законы природы не зависят от исследователя, то тесты в немалой степени зависят от его воли. Это принципиально важный момент.
IRT в настоящий момент является общепризнанной теорией. В качестве латентных параметров модели выступают как характеристики тестируемых, так и самого теста. Ю. Нейман и В. Хлебников делают вывод, что «…уникальность моделей семейства Г. Раша состоит в том, что они задают определенный механизм преобразования формальных наблюдений за исходом событий в объективные измерения на метрической шкале латентных стимулов этих событий». Это очень важно, так как недостаточно глубокое осознание этого факта, может приводить к тому, что положения педагогических измерений могут критически восприниматься специалистами в области точных наук. Таким образом, несоответствие эмпирических данных модели Раша означает, что, например, имеются неточности в формулировке заданий, были нарушения в процедуре тестирования и т.д.
Как отмечает В.C.Аванесов, в литературе можно встретить немало критики по поводу неприменимости модели Раша к множеству «тестов», и поэтому ведется поиск других моделей, более адекватных полученным результатам. Но здесь есть один очень важный вопрос. В теории Г .Раша никогда не ставилась задача адекватного описания данных. Напротив, это пример другой философии измерения - model based measurement, где утверждается противоположное – не модель должна соответствовать эмпирическим данным, а данные должны соответствовать модели. Об этом можно спорить, но в соответствии с философией Rasch шкалу (педагогический тест) образуют только те задания, которые отвечают данной модели измерения. Все остальные в тест не включаются.
Итак, при анализе результатов тестирования, необходимо проверить соответствие эмпирических данных модели Раша. Согласно Ф. Бейкеру для этого всех N тестируемых, выполняющих К - заданий теста распределяют по шкале θ (ability) по своим диапазонам уровня подготовленности. Испытуемые делятся на J групп вдоль шкалы θ так, чтобы все тестируемые внутри данной группы имели одинаковый уровень подготовленности θj. Всего внутри группы с номером j окажутся mj тестируемых, где j принимает значения из интервала j = 1,2,3,…,J.
В пределах каждой группы rj тестируемых отвечают правильно на данное задание теста. Таким образом, для уровня подготовленности (уровня знаний) равного θj вероятность правильного ответа на данное задание равна
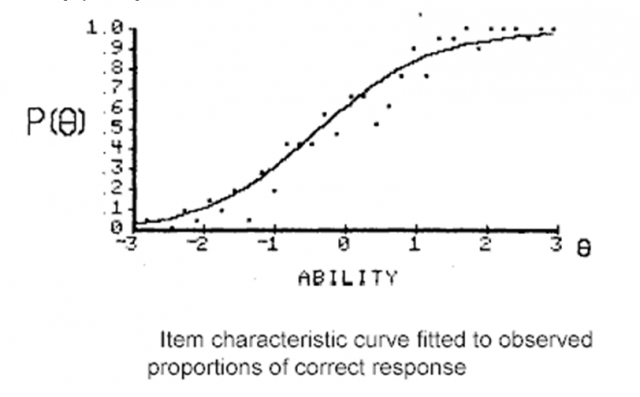
Величина p(θj) является эмпирическим значением вероятности правильного ответа на данное задание. На рисунке 1 показаны данные из работы F. Baker (2001).
На следующем этапе проверяется, насколько хорошо эмпирические данные описываются IRT-моделью. Результат сравнения показан на рисунке 2.
Из рисунка 2 видно, что наблюдается хорошее согласие эмпирических данных с IRT. В целом задача разработчика тестов состоит в том, чтобы разработать такие тестовые задания и так осуществить процедуру тестирования, чтобы получить результаты, аналогичные тем, что показаны на рисунке 2.
Основные результаты работы.
В данной работе приведены результаты тестирования учащихся средних общеобразовательных учреждений по теме «Механика» учебной дисциплины «Физика». Тест содержал 30 заданий с выбором одного правильного ответа. Всего было протестировано 60 испытуемых, по итогам была составлена . бинарная матрица размером 60х30. После упорядочения матрицы по строкам и столбцам по стандартной процедуре были рассчитаны логистические кривые по одномерной модели Раша.
Для модели Раша вероятность успеха в j-м задании равна
где d – фактор шкалирования, равный 1,702.
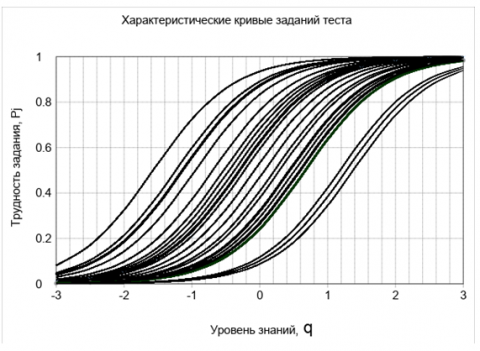
На рисунке 3 приведены результаты расчетов для всех 30 заданий теста.
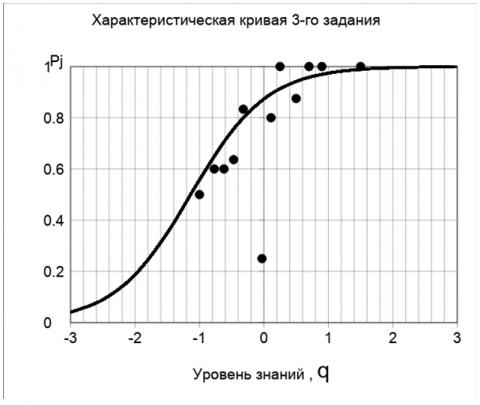
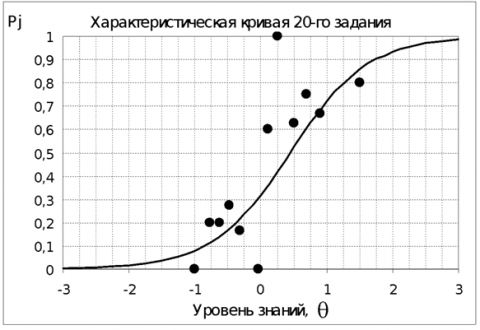
Экспериментальные значения Pj, полученные по методике4, приведены на рисунках 4-7. Экспериментальные данные показаны выборочно для четырех заданий различного уровня трудности – 3, 8, 20, 30 задания.
Обсуждение полученных результатов.
По результатам тестирования сразу можно получить матрицу, анализируя которую можно избавить тест от некоторых неподходящих заданий. Дальнейшие расчеты возможны в трех вариантах:
Однопараметрическая (одномерная) логистическая модель, или модель Раша;
Двухпараметрическая логистическая модель (2PL) Бирнбаума;
Трехпараметрическая логистическая модель (3PL) Бирнбаума.
Как известно, модели 2PL и 3PL предлагались для лучшего согласования теории с наблюдаемыми эмпирическими данными. Если считать, что согласования следует добиваться не видоизменением теории, а получением других эмпирических данных, то можно остановиться на модели Раша. Иными словами, если экспериментальные данные не соответствуют модели Раша, то необходимо переработать тестовые задания и повторно провести эксперимент, добиваясь лучшего согласия с теорией, как указывалось выше.
Следуя такой парадигме, в данной работе все построения проводились по модели Г. Раша.
Из рисунка 3 видно, что задания теста по шкале уровня знаний θ перекрывают диапазон примерно от -3,5 до +3,5 логитов. Графики показаны последовательно слева- направо от 1-го (самого легкого) до 30-го самого трудного задания. Характеристические кривые некоторых заданий, а именно 3 и 4; 10 и 11; 13, 14 и 15; 19, 20 и 21; 23 и 24; 25, 26 и 27 перекрываются. В связи с этим 4, 11, 14, 15, 19, 21, 24, 26, 27 задания могут быть удалены из теста без ущерба его измерительным свойствам.
На семействе логистических кривых тестовых заданий отчетливо наблюдается явная недостаточность отдельных заданий. Наличие «провалов» в монотонной последовательности характеристических кривых указывает на необходимость дополнительной оптимизации теста путем добавления новых тестовых заданий или переработки имеющихся. Переработкой тестовых заданий необходимо добиться появления добавочных характеристических кривых в интервале от -1,5 до - 0,5 и от +0,7 до +1,2 логита (на уровне Pj = 0,5).
Экспериментальные данные для Pj имеют примерно одинаковое согласие с моделью Раша, которое можно считать удовлетворительным. Приведенные на рисунках 4-7 характеристические кривые некоторых заданий иллюстрируют это. При анализе вся совокупность тестируемых разбивалась на 12 групп (J=12).
Экспериментальные точки для характеристической кривой 3-го задания группируются в области от -1 до +1 логита для Pj от 0,5 до 1,0. Это относительно легкое задание и экспериментальные точки приблизительно соответствуют верхнему участку характеристической кривой. Задания 8 и 20 находятся примерно в средней области тестовых заданий (рисунок 3) и соответствуют заданиям средней сложности. Экспериментальные точки в этом случае группируются вблизи линейной области характеристических кривых P8 и P20
Задание №30 самое трудное и экспериментальные точки в основном сосредоточены вблизи нижнего загиба характеристической кривой P30.
Для проверки гипотезы Ho на соответствие полученных эмпирических данных одномерной модели IRT для всех заданий теста проводилось вычисление критерия χ2 согласно
Расчетное значение критерия χ2 оказалось в пределах от 7 до 15 для различных заданий теста.
Таким образом, несмотря на довольно заметную вариацию данных, что вероятнее всего обусловлено недостаточной репрезентативностью выборки (60 испытуемых), можно констатировать удовлетворительное согласие экспериментальных результатов с Rasch Measurement.
[1] Rasch G. Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen, 1960, Danish Institute of Educational Research. (Expanded edition, Chicago, 1980, The University of Chicago Press). [3]Аванесов В.С. Применение тестовых форм в Rasch Measurement. См. статью в номере ПИ №4, 2005г. [4] Baker F.B. The Basics of Item Response Theory. –ERIC, 2001. -172 p [5] Аванесов В.С. Форма тестовых заданий. М. Центр тестирования, 2005. [6] . Аванесов В.С. Основы научной организации педагогического контроля в высшей школе. М., 1989. -167 с. [7] Rasch G. Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen, 1960, Danish Institute of Educational Research. (Expanded edition, Chicago, 1980, The University of Chicago Press). [8] Baker F.B. The Basics of Item Response Theory. –ERIC, 2001. -172 pПерсоны (1)
1463130